NAGVAC

Fit VBLab supported or custom models using the NAGVAC method

Syntax

Post = NAGVAC(Mdl,data,Name,Value)

Description

EstMdl = NAGVAC(Mdl,data,Name,Value) runs the NAGVAC algorithm to return the estimation results Post given the model Mdl and data data. The model Mdl can be a VBLab supported or custom model. The custom models can be defined as class objects or function handles. Name and Value specify additional options using one or more name-value pair arguments. For example, you can specify how many samples used to estimate the lower bound.

See: Input Arguments, Output Argument, Examples

Input Arguments

Mdl - VBLab supported or custom model objects

Data type: VBLab model object | custome model object | function handle

The statistical models containing unknown parameters, can be specified as:

data - Input data

Data type: 2D array | 1D array | table

The data to which the model Mdl or Func is fitted, specified as a table or matrix.

For cross-sectional data, NAGVAC takes the last variable as the response variable and the others as the predictor variables.

For time series data, the data can be stored in a row or column 1D array.

Name-Value Pair Arguments

Specify optional comma-separated pairs of Name,Value arguments. Name is the argument name and Value is the corresponding value. Name must appear inside quotes. You can specify several name and value pair arguments in any order as Name1,Value1,...,NameN,ValueN.

Example: 'LearningRate',0.001,'LBPlot',true specifies that the learning rate of the NAGVAC algorithm is set to be $0.001$ and the plot of the covergence of the lowerbound is shown at the end of the algorithm.

Name	Default Value	Notation	Description
`'GradWeight'`	`0.9`	$\alpha_m$	Momentum weight
`'GradientMax'`	`10`	$\ell_\text{threshold}$	Gradient clipping threshold
`'InitValue'`	`None`		Initial values of varitional mean
`'LBPlot'`	`true`		Flag to plot the lowerbound or not
`'LearningRate'`	`0.01`	$\epsilon_0$	Fixed learning rate
`'MaxIter'`	`1000`		Maximum number of iterations
`'MaxPatience'`	`20`	$P$	Maximum patience for early stopping
`'NumSample'`	`50`	$S$	Monte Carlo samples to estimate the lowerbound
`'NumParams'`	`None`		Number of model parameters
`'SaveParams'`	`false`		Flag to save training parameters or not
`'Setting'`	`None`		Additional setting for custom models
`'SigInitScale'`	`0.1`		Constant factor for initialization
`'StdForInit'`	`0.01`		Standard deviation of normal distribution for initialization
`'StepAdaptive'`	`'MaxIter'/2`	$\tau$	Threshold to start reducing learning rates
`'TrainingLoss'`	`PPS`		Training loss over VB iterations
`'Validation'`	`0.1`		Subset of training data used for validation
`'ValidationLoss'`	`PPS`		Validation loss over VB iterations
`'Verbose'`	`true`		Flag to show real-time fitting information or not
`'WindowSize'`	`50`		Rolling window size to smooth the lowerbound

'GradWeight' - Momentum weight

Data Type: Double

The momentum weight $\alpha_m$ in Algorithm 9,

Must be a number between $0$ and $1$.

Default: 0.9

Example: 'GradWeight',0.95

'GradientMax' - Gradient clipping threshold

Data Type: Double | Positive

The maximum value to prevent the exploding gradient problem that occurs when the gradient gets too large, thus making the optimization for the model parameters (e.g., using gradient descent) highly unstable.

Default: 100

Example: 'GradientMax',10

'InitValue' - Initial values of varitional mean

Data Type: Column vector

The column vector of initial values of variational parameters. For example, we can use the point estimation of model parameters from MLE to initialize the VB techniques.

Default: None

Example: 'InitValue',zeros(D,1)

'LBPlot' - Flag to plot the lowerbound or not

Data Type: True | False

Flag to plot the smoothed lowerbound over iterations to quicly check the convergence of the VB algorithm.

Default: true

Example: 'LBPlot',false

'LearningRate' - Fixed learning rate

Data Type: Double | Between 0 and 1

The fixed learning rate $\epsilon_0$ to update the variational parameters in each VB iteration in Algorithm 9.

Must be a number between $0$ and $1$.

Default: 0.01

Example: 'LearningRate',0.001

'MaxIter' - Maximum number of iterations

Data Type: Integer | Positive

Maximum number of VB iterations for early stopping. If the 'BatchSize' argument is specified, users have to use the 'MaxEpoch' argument to specify the maximum number of iterations instead.

Default: 1000

Example: 'MaxIter',1000

'MaxPatience' - Maximum patience for early stopping

Data Type: Integer | Positive

Number of consecutive times that the validation loss, or lowerbound, is allowed to be larger than or equal to the previously smallest loss, or lowerbound, before the training is stopped, used as an early stopping criterion. This is denoted as $P$ in Algorithm 9.

Default: 20

Example: 'MaxPatience',100

'NumSample' - Monte Carlo samples to estimate the lowerbound

Data Type: Integer | Positive

Number of Monte Carlo samples needed to estimate the gradient of the lower bound. This is denoted as $S$ in Algorithm 9.

Default: 50

Example: 'NumSample',100

'NumParams' - Number of model parameters

Data Type: Integer | Positive

Number of model parameters.

If the handle of the function calculating the $h(\theta)$ and $\nabla_\theta h(\theta)$ terms is provided, users have to specify a value for this argument.
If a model object is specified, users have to set the number of parameters using the NumParams property of the model class. See how to define a custom model as a Maltab class object.

Default: None

Example: 'NumParams',{'Normal',[0,10]}

'SaveParams' - Flag to save training parameters or not

Data Type: true | false

Flag to save variational parameters in each VB iteration.

Default: false

Example: 'SaveParams',true

'Setting' - Additional setting for custom models

Data Type: struct

Additional settings that could be use to define custom models as function handlers.

The most efficient way is to define these additional setting as a struct. This struct then will be passed to the function handlers as an input. See how to define custom model as function handler.

Default: None

Example: 'Setting',prior with prior is a struct whose fields are prior distribution name and parameters, e.g. prior.name = 'Normal' and prior.params = [0,1].

'SigInitScale' - Constant factor for initialization

Data Type: double

The constant factor $c$ to scale the initial values.

Default: 0.1

Example: 'SigInitScale',0.5

'StdForInit' - Standard deviation of normal distribution for initialization

Data Type: double

The constant factor $\sigma$ to scale the convariance matrix of the normal distribution used to initialize the variational mean.

Only specify this argument when the argument 'InitMethod' is set to 'Random'.

Default: 0.01

Example: 'StdForInit',0.04

'StepAdaptive' - Threshold to start reducing learning rates

Data Type: Integer | Positive

The iteration to start reducing learning rate, which is denoted as $\tau$ in Algorithm 9.

By default, this is set as 'MaxIter'/2 or 'MaxEpoch'/2.

Must be smaller than 'MaxIter' or 'MaxEpoch'.

Default: 'MaxIter'/2 or 'MaxEpoch'/2

Example: 'StepAdaptive',300

'TrainingLoss' - Training loss over VB iterations

Data Type: string | cell array of strings

The VB algorithm uses lowerbound to access the convergence of the training phase.

However, users can also calculate the predictive scores evaluated on the training data over VB iterations. Users can specify a single metric, defined as a string, or multiple metrics, defined as a cell array of strings.

Available score metrics:

PPS	Partial Predictive Score
MSE	Mean Squared Errors (for continuos output)
MAE	Mean Absoluted Errors (for continuos output)
CR	Classification rate (for binary output)

For the PPS:

If the models are specified as function handlers, users have to also specify function handlers to the argument 'LogLikFunc' to compute the log-likelihood of the custom models.
If the models are specified as class objects, users have to define a method named logLik() to compute the log-likelihood of the custom models.

Default: None

Example: 'TrainingLoss',{'PPS','MSE'}

'Validation' - Subset of training data used for validation

Data Type: double between 0 and 1 | Integer

Number of observations of training data are used as validation data. The number of observations can be specified as a percentage (a number between 0 and 1) of training data or an integer smaller than the number of training observations.

Note: This option is only available for cross-sectional (tabular) data.

Default: None

Example: 'Prior',0.1 or 'Prior',1000

'ValidationLoss' - Validation loss computed during fitting phase

Data Type: string | cell array of strings

Calculate the predictive scores evaluated on the validation data over VB iterations. Users can specify a single metric, defined as a string, or multiple metrics, defined as a cell array of strings.

Available score metrics:

PPS	Partial Predictive Score
MSE	Mean Squared Errors (for continuos output)
MAE	Mean Absoluted Errors (for continuos output)
CR	Classification rate (for binary output)

For the PPS:

If the models are specified as function handlers, users have to also specify function handlers to the argument 'LogLikFunc' to compute the log-likelihood of the custom models.
If the models are specified as class objects, users have to define a method named logLik() to compute the log-likelihood of the custom models.

Note: This option is only available for cross-sectional (tabular) data.

Default: None

Example: 'ValidationLoss','MSE'

'Verbose' - Flag to show real-time fitting information or not

Data Type: True | False

By default, the index of the current iteration and lowerbound are shown in every iteration. Set 'Verbose' to be false to turn off these messages.

Default: true

Example: 'Verbose',false

'WindowSize' - Rolling window size to smooth the lowerbound

Data Type: Integer | Positive

Size of moving average window that used to smooth the lowerbound. Denoted as $t_W$ in Algorithm 9.

Default: 50

Example: 'WindowSize',100

Output Arguments

Post - Estimation results

Data type: struct

Estimation results, specified as a structure with these fields:

LB	Estimation of the Lower Bound over iterations
LB_smooth	Smoothed Lower Bound over iterations
lambda	Estimation of variational parameters
mu	Estimation of variational mean
b	The vector factor loading vector component of the variational covariance matrix
C	The diagonal matrix component of the variational covariance matrix
Sigma	Estimation of the variational covariance matrix
sigma2	Diagonal of the variational covariance matrix

Examples Github code

This example shows how to use NAGVAC to fit a logistic regression model on the LabourForce dataset. First, Load the LabourForce data as a matrix. The last column is the response variable.

% Random seed to reproduce results 
rng(2020)

% Load LabourForce data. 
labour = readData('LabourForce',...     % Dataset name
                  'Type','Matrix',...   % Store data as a 2D array (default)
                  'Intercept', true);   % Add column of intercept (default)

Create a LogisticRegression model object by specifying the number of parameters as the input argument. Change the variance of the normal prior to $50$.

% Compute number of features
n_features = size(labour,2)-1;

% Create a Logistic Regression model object
Mdl = LogisticRegression(n_features,...
                        'Prior',{'Normal',[0,50]});

Run NAGVAC to obtain VB approximation of the posterior distribution of model parameters. We use $200$ samples to estimate the gradient of lowerbound.

%% Run NAGVAC with random initialization
Post_NAGVAC = NAGVAC(Mdl,labour,...
                    'NumSample',200,...       % Number of samples to estimate gradient of lowerbound
                    'LearningRate',0.005,...  % Learning rate
                    'MaxPatience',20,...      % For Early stopping
                    'MaxIter',10000,...       % Maximum number of iterations
                    'GradientMax',200,...     % For gradient clipping    
                    'WindowSize',50, ...      % Smoothing window for lowerbound
                    'LBPlot',true);           % Dont plot the lowerbound when finish

Given the estimation results, we can plot the variational distribution together with the lowerbound to check the performance of the NAGVAC algorithm.

%% Plot variational distributions and lowerbound 
figure
% Extract variation mean and variance
mu_vb     = Post_NAGVAC.Post.mu;
sigma2_vb = Post_NAGVAC.Post.sigma2;

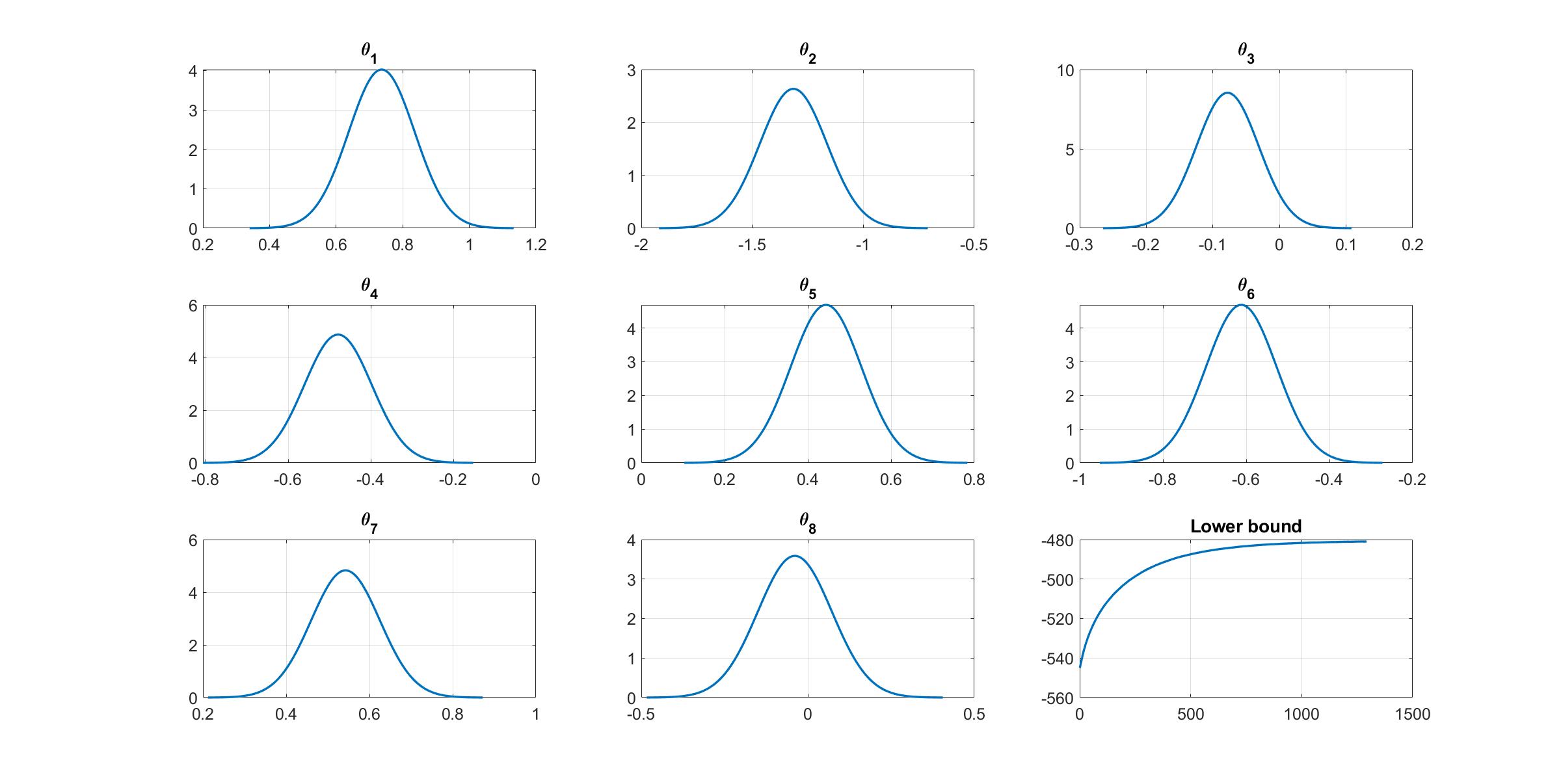
% Plot the variational distribution for the first 8 parameters
for i=1:n_features
    subplot(3,3,i)
    vbayesPlot('Density',{'Normal',[mu_vb(i),sigma2_vb(i)]})
    grid on
    title(['\theta_',num2str(i)])
    set(gca,'FontSize',15)
end

% Plot the smoothed lower bound
subplot(3,3,9)
plot(Post_NAGVAC.Post.LB_smooth,'LineWidth',2)
grid on
title('Lower bound')
set(gca,'FontSize',15)   

The plot of lowerbound shows that the NAGVAC algorithm works properly.

Reference

[1] Tran, M.-N., Nguyen, T.-N., Nott, D., and Kohn, R. (2020). Bayesian deep net GLM and GLMM. Journal of Computational and Graphical Statistics, 29(1):97-113. Read the paper

NAGVAC

Syntax

Description

Input Arguments

Data type: VBLab model object | custome model object | function handle

Data type: 2D array | 1D array | table

Data Type: Double

Data Type: Double | Positive

Data Type: Column vector

Data Type: True | False

Data Type: Double | Between 0 and 1

Data Type: Integer | Positive

Data Type: Integer | Positive

Data Type: Integer | Positive

Data Type: Integer | Positive

Data Type: true | false

Data Type: struct

Data Type: double

Data Type: double

Data Type: Integer | Positive

Data Type: string | cell array of strings

Data Type: double between 0 and 1 | Integer

Data Type: string | cell array of strings

Data Type: True | False

Data Type: Integer | Positive

Output Arguments

Data type: struct

Examples Github code

Reference

See Also